二叉树属性

一个有效的树中，如果有N个节点就会有N-1条边。

深度：树的节点X的深度被定义为从根到节点X的路径长度。路径上的每一条边贡献一个长度单位。根的深度是0。

高度：树的节点X的高度被定义为从该节点到一个叶子节点的最长路径上的边数。叶子节点的高度是0。

树的高度：树的高度等于根节点的高度。

二叉树：一个树中的每个节点最多含有两个子节点(children) ，这个树被称为二叉树。

树的实现方式：动态创建节点，用指针或者引用把他们链接起来。

二叉树：每个节点有三个域，其中一个用来存放数据，其它两个为指向节点的指针。一个存储左孩的地址，另一个存储右孩的地址。

# 二叉树属性题

# 1.1.对称二叉树 (opens new window)

给你一个二叉树的根节点 root ，检查它是否轴对称。

示例 1：
输入：root = [1,2,2,3,4,4,3]
输出：true
1
2
示例 2：
输入：root = [1,2,2,null,3,null,3]
输出：false
1
2

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
  def isSymmetric(self, root: Optional[TreeNode]) -> bool:
      if not root:
          return False
      if (not root.left) ^( not root.right):
          return False
      
      queue = collections.deque([root.left, root.right])
      while queue:
          cur1 = queue.popleft()
          cur2 = queue.popleft()
          if (not cur1) ^ (not cur2):
              return False
          if cur1 and cur2:
              if cur1.val != cur2.val:
                  return False
              queue.append(cur1.left)
              queue.append(cur2.right)
              queue.append(cur1.right)
              queue.append(cur2.left)
      return True

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

// Make sure to add code blocks to your code group

# 1.2二叉树的最大深度 (opens new window)

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：
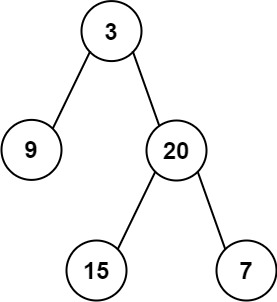
输入：root = [3,9,20,null,null,15,7]
输出：3
1
2
示例 2：
输入：root = [1,null,2]
输出：2
1
2

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
  def maxDepth(self, root: Optional[TreeNode]) -> int:
      """
      广度优先遍历，最大深度就是遍历的层数
      """
      if not root:
          return 0
      queue = collections.deque([root])
      ret = 0
      while queue:

          for _ in range(len(queue)):
              node = queue.popleft()
              if node.left:
                  queue.append(node.left)
              if node.right:
                  queue.append(node.right)
          ret += 1
      return ret

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
  def maxDepth(self, root: Optional[TreeNode]) -> int:
      """
      深度优先遍历
      """
      def height(root):
          if not root:
              return 0
          return max(height(root.left), height(root.right))+1
      return height(root)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

// Make sure to add code blocks to your code group

# [1.3.二叉树的最小深度](111. 二叉树的最小深度 - 力扣（LeetCode） (opens new window))

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

**说明：**叶子节点是指没有子节点的节点。

示例 1：
输入：root = [3,9,20,null,null,15,7]
输出：2
1
2
示例 2：
输入：root = [2,null,3,null,4,null,5,null,6]
输出：5
1
2
提示：

树中节点数的范围在 [0, 105] 内

-1000 <= Node.val <= 1000

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
  def minDepth(self, root: Optional[TreeNode]) -> int:
      if not root:
          return 0
      left = root.left
      right = root.right
      min_depth = float("inf")
      if not left and not right:
          return 1

      if left:
          min_depth = min(self.minDepth(left), min_depth)
      if right:
          min_depth = min(self.minDepth(right), min_depth)
      return min_depth + 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

/**
* Definition for a binary tree node.
* type TreeNode struct {
*     Val int
*     Left *TreeNode
*     Right *TreeNode
* }
*/

func minDepth(root *TreeNode) int {
  var height func(root *TreeNode) int 
  height = func(root *TreeNode) int{
      if root == nil{
          return 0
      }
      if (root.Left == nil) && (root.Right == nil){
          return 1
      }
      minD := math.MaxInt32
      if root.Left != nil{
          minD = min(height(root.Left), minD)       
      }
      if root.Right != nil{
          minD = min(height(root.Right), minD)
      }
      return minD + 1
  }
  return height(root) 
}

func min(a, b int ) int{
  if a>b{
      return b 
  } else{
      return a
  }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

// Make sure to add code blocks to your code group

# 1.4. 完全二叉树的节点个数 (opens new window)

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 (opens new window) 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

示例 1：
输入：root = [1,2,3,4,5,6]
输出：6
1
2
示例 2：
输入：root = []
输出：0
1
2
示例 3：
输入：root = [1]
输出：1
1
2

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
  def maxDepth(self, root: Optional[TreeNode]) -> int:
      """
      深度优先遍历
      """
      def height(root):
          if not root:
              return 0
          #return max(height(root.left), height(root.right))+1
          # 上面的写法等价于
          leftdepth = height(root.left) +1
          rightdepth = height(root.right) + 1
          return max(leftdepth, rightdepth)
      return height(root)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

// Make sure to add code blocks to your code group

# 1.5. 平衡二叉树 (opens new window)

给定一个二叉树，判断它是否是

平衡二叉树

示例 1：
输入：root = [3,9,20,null,null,15,7]
输出：true
1
2
示例 2：
输入：root = [1,2,2,3,3,null,null,4,4]
输出：false
1
2
示例 3：
输入：root = []
输出：true
1
2

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
  def isBalanced(self, root: Optional[TreeNode]) -> bool:
      # 左右子树高度不超过1
      
      def depth(root: Optional[TreeNode]) -> int:
          if not root:
              return 0
          leftdepth = depth(root.left) + 1
          rightdepth = depth(root.right) + 1
          return max(leftdepth, rightdepth)
      
      # 如果这个树是二叉树，左右子树高度差< 1, 并且左右子树均为二叉树
      if not root:
          return True
      return True if (abs(depth(root.left)- depth(root.right))<=1 and self.isBalanced(root.left) and self.isBalanced(root.right)) else False

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

// Make sure to add code blocks to your code group

# 1.6二叉树的所有路径 (opens new window)

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

示例 1：
输入：root = [1,2,3,null,5]
输出：["1->2->5","1->3"]
1
2
示例 2：
输入：root = [1]
输出：["1"]
1
2

笔记

递归+回溯

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
  def binaryTreePaths(self, root: Optional[TreeNode]) -> List[str]:

      ret = list()
      def dfs(root, path):
          if not root:
              return
          path.append(str(root.val))
          if root.left==None and root.right == None:
              ret.append( "->".join(path[:]))
              return
          if root.left:
              dfs(root.left, path)
              path.pop()
          if root.right:
              dfs(root.right, path)
              path.pop()
      dfs(root,[])
      return ret

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

/**
* Definition for a binary tree node.
* type TreeNode struct {
*     Val int
*     Left *TreeNode
*     Right *TreeNode
* }
*/
func binaryTreePaths(root *TreeNode) []string {
  
  ret := make([]string, 0)
  path := make([]string, 0)
  var dfs func(root *TreeNode)
  dfs = func(root *TreeNode){
      if root == nil{
          return
      }
      path = append(path, strconv.Itoa(root.Val))
      if root.Left == nil && root.Right == nil{
          temp := make([]string, len(path))
          copy(temp, path)
          ret = append(ret, strings.Join(temp, "->"))
          return
      }
      if root.Left != nil{
          dfs(root.Left)
          path = path[:len(path)-1]
      }
      if root.Right != nil{
          dfs(root.Right)
          path = path[:len(path)-1]
          
      }
  }
  dfs(root)
  return ret
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

// Make sure to add code blocks to your code group

# 1.7.左叶子之和 (opens new window)

给定二叉树的根节点 root ，返回所有左叶子之和。

示例 1：

输入: root = [3,9,20,null,null,15,7] 
输出: 24 
解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

1
2
3

示例 2:

输入: root = [1]
输出: 0

1
2

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Solution:
  def sumOfLeftLeaves(self, root: Optional[TreeNode]) -> int:
      
      def dfs(root, isLeft):
          if not root:
              return 0
          ret = 0
          if (not root.left)  and (not root.right) and (isLeft):
              ret = ret + root.val
              return ret

          if root.left:
              ret +=dfs(root.left, True)
          if root.right:
              ret += dfs(root.right, False)
          return ret
      ret = dfs(root, False)
      return ret

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

class Solution:
  def sumOfLeftLeaves(self, root: Optional[TreeNode]) -> int:
      ret = 0
      def dfs(root):
          if not root:
              return 0
          ret = 0
          if (root.left)  and (not root.left.left) and (not root.left.right):
              ret = ret + root.left.val
          ret += dfs(root.left)
          ret += dfs(root.right)
          return ret
      ret = dfs(root)
      return ret

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

/**
* Definition for a binary tree node.
* type TreeNode struct {
*     Val int
*     Left *TreeNode
*     Right *TreeNode
* }
*/
func sumOfLeftLeaves(root *TreeNode) int {
  ans := 0
  var dfs func(node *TreeNode, isLeft bool)
  dfs = func(node *TreeNode, isLeft bool){
      if node == nil{
          return 
      }
      if isLeft== true && node.Left == nil && node.Right ==nil{
          ans +=  node.Val
      }
      dfs(node.Left, true)
      dfs(node.Right, false)
      return
  }
  dfs(root, false)
  return ans
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

/**
* Definition for a binary tree node.
* type TreeNode struct {
*     Val int
*     Left *TreeNode
*     Right *TreeNode
* }
*/
func sumOfLeftLeaves(root *TreeNode) int {
  ans := 0
  var dfs func(node *TreeNode)
  dfs = func(node *TreeNode){
      if node == nil{
          return
      }
      if node.Left != nil && node.Left.Left == nil && node.Left.Right ==nil{
          ans +=  node.Left.Val
      }
      dfs(node.Left)
      dfs(node.Right)
      return
  }
  dfs(root)
  return ans
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

// Make sure to add code blocks to your code group

# 1.8找树左下角的值 (opens new window)

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层最左边 节点的值。

假设二叉树中至少有一个节点。

示例 1:
输入: root = [2,1,3]
输出: 1
1
2
示例 2:
输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7
1
2

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
  def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:

      queue = collections.deque([root])
      while queue:
          temp = collections.deque()
          for i in range(len(queue)):
              cur = queue[i]
              if cur.left:
                  temp.append(cur.left)
              if cur.right:
                  temp.append(cur.right)
          if len(temp)==0:
              break
          queue = temp
      return queue[0].val

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

/**
* Definition for a binary tree node.
* type TreeNode struct {
*     Val int
*     Left *TreeNode
*     Right *TreeNode
* }
*/
func findBottomLeftValue(root *TreeNode) int {

  // 层序遍历取最后一层的第一个
  queue := []*TreeNode{}
  
  queue = append(queue, root)
  for len(queue)>0{
      temp := []*TreeNode{}
      n := len(queue)
      for i:=0;i<n;i++{
          cur := queue[i]
          if cur.Left != nil{
              temp = append(temp, cur.Left)
          }
          if cur.Right != nil{
              temp = append(temp, cur.Right)
          }
      }
      if len(temp) == 0{
          break
      }
      queue = temp
  }
  return queue[0].Val
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

// Make sure to add code blocks to your code group

# 1.9.路径总和 (opens new window)

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

示例 1：
输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。
1
2
3
示例 2：
输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。
1
2
3
4
5
6
示例 3：
输入：root = [], targetSum = 0
输出：false
解释：由于树是空的，所以不存在根节点到叶子节点的路径。
1
2
3

// Make sure to add code blocks to your code group

# 1.10路径总和 (opens new window)

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

示例 1：
输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。
1
2
3
示例 2：
输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。
1
2
3
4
5
6
示例 3：
输入：root = [], targetSum = 0
输出：false
解释：由于树是空的，所以不存在根节点到叶子节点的路径。
1
2
3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
  def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
      if not root:
          return False
      def dfs(root, num):
          if root == None:
              return False
          
          if root.left == None and root.right == None and num == targetSum:
              return True 
          
          if root.left:
              tag = dfs(root.left, num + root.left.val)
              if tag:
                  return True
          if root.right:
              tag  = dfs(root.right, num + root.right.val)
              if tag:
                  return True
          return False
      return dfs(root, root.val)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
  def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
      if not root:
          return False
      queue1 = collections.deque([root])
      queue2 = collections.deque([root.val])

      while queue1:
          cur = queue1.popleft()
          num = queue2.popleft()
          if cur.left == None and cur.right==None and num == targetSum:
              return True
          if cur.left:
              queue1.append(cur.left)
              queue2.append(num + cur.left.val)
          if cur.right:
              queue1.append(cur.right)
              queue2.append(num+cur.right.val)
      return False

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

/**
* Definition for a binary tree node.
* type TreeNode struct {
*     Val int
*     Left *TreeNode
*     Right *TreeNode
* }
*/
func hasPathSum(root *TreeNode, targetSum int) bool {
  // 深度优先算法
  if root == nil{
      return false
  }
  var dfs func(root *TreeNode, num int) bool
  dfs = func(root *TreeNode, num int) bool {
      if root == nil{
          return false
      }
      if root.Left == nil && root.Right == nil && num == targetSum{
          return true
      }
      if root.Left != nil{
          tag := dfs(root.Left, num + root.Left.Val)
          if tag == true{
              return true
          }
      }
      if root.Right != nil{
          tag := dfs(root.Right, num + root.Right.Val)
          if tag == true{
              return true
          }
      }
      return false
  }
  return dfs(root, root.Val)
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

/**
* Definition for a binary tree node.
* type TreeNode struct {
*     Val int
*     Left *TreeNode
*     Right *TreeNode
* }
*/
func hasPathSum(root *TreeNode, targetSum int) bool {
  // 广度优先算法
  if root == nil{
      return false
  }
  queue1 := []*TreeNode{root}
  queue2 := []int{root.Val}
  for len(queue1)>0{
      cur := queue1[0]
      num := queue2[0]
      queue1 = queue1[1:]
      queue2 = queue2[1:]

      if num == targetSum && cur.Left == nil && cur.Right == nil{
          return true
      }
      if cur.Left != nil{
          queue1 = append(queue1, cur.Left)
          queue2 = append(queue2, num + cur.Left.Val)
      }
      if cur.Right != nil{
          queue1 = append(queue1, cur.Right)
          queue2 = append(queue2, num + cur.Right.Val)
      }

  }
  return false
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

// Make sure to add code blocks to your code group

编辑

上次更新: 2024/12/13 19:48:29

← 二叉搜索树二叉树修改与构造→